Included Decision Trees
Three decision trees are currently distributed with tedana.
meica is the decision tree that is based on MEICA version 2.5 and
tedana_orig is very similar and has been included with tedana
since the start of this project. An explanation of why these both exist
is in the FAQ
While multiple publications have used and benefited from this decision,
tree, but it includes many steps with arbitrary thresholds and, when
components seem misclassified, it’s often hard to understand why.
minimal is a simplified version of that decision tree with fewer
steps and arbitrary thresholds. Minimal is designed to be more stable
and comprehensible, but it has not yet be extensively validated and
parts of the tree may change in response to additional tests on a
wider range of data sets.
Flowcharts describing the steps in both trees are below.
As documented more in Understanding and building a component selection process, the input to each tree
is a table with metrics, like  or
or 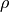 , for each
component. Each step or node in the decision tree either calculates
new values or changes component classifications based on these metrics.
When a component classification changes to
, for each
component. Each step or node in the decision tree either calculates
new values or changes component classifications based on these metrics.
When a component classification changes to accept or reject, a
classification_tag is also assigned which may help understand why
a component was given a specific classification.
Each step in the flow chart is labeled with a node number.
If tedana is run using one of these trees, those node
numbers will match the numbers in the ICA status table and the
ICA decision tree that are described in
Output filename descriptions. These node numbers can be used
to see when in the process a component’s classifiation changed.
meica decision tree
Nodes 1-5 reject components that are very unlikely to be BOLD.
In nodes 9-10 components where  >
>
 elbow and
elbow and 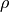 <
< 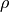 elbow are classified as provisional accept. A non-obvious aspect
of this decision tree is that no decision node below this point distinguishes
components that are provisional accept from components that are still
unclassified and nothing that does not cross the
elbow are classified as provisional accept. A non-obvious aspect
of this decision tree is that no decision node below this point distinguishes
components that are provisional accept from components that are still
unclassified and nothing that does not cross the  and
and
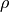 elbow thresholds is inherantly rejected. The number of
provisional accept components is used to see if the process should
be restarted (node 11) and calculate other thresholds (nodes 12-16 & 20),
but nothing is directly accepted or rejected based on the elbow thresholds.
Several additional criteria are used to reject components (nodes 17, 21, & 22).
In older versions of
elbow thresholds is inherantly rejected. The number of
provisional accept components is used to see if the process should
be restarted (node 11) and calculate other thresholds (nodes 12-16 & 20),
but nothing is directly accepted or rejected based on the elbow thresholds.
Several additional criteria are used to reject components (nodes 17, 21, & 22).
In older versions of tedana components were classified as ignored.
This meant too small/minor to lose a degree of freedom by rejecting so treat
like the accepted components. This was widely confusing to many users so they
are now classified as accepted but with classification tags low variance
(node 18) or accept borderline (nodes 24 & 25).

tedana_orig decision tree
Identical to the meica decision tree until node 21. In the tedana tree, components that cross the threshold criteria in nodes 21 and 22 are rejected and not included in the calculation for a new variance explained threshold in node 23. In the meica tree, those components are provisionally rejected, but still included in the new variance explained calculation and can be potentially accepted in nodes 24 and 25. This means tedana will give the same results as meica or reject additional components base on those two final decision criteria.

LaTeX file to generate the tedana_orig decision tree flow chart
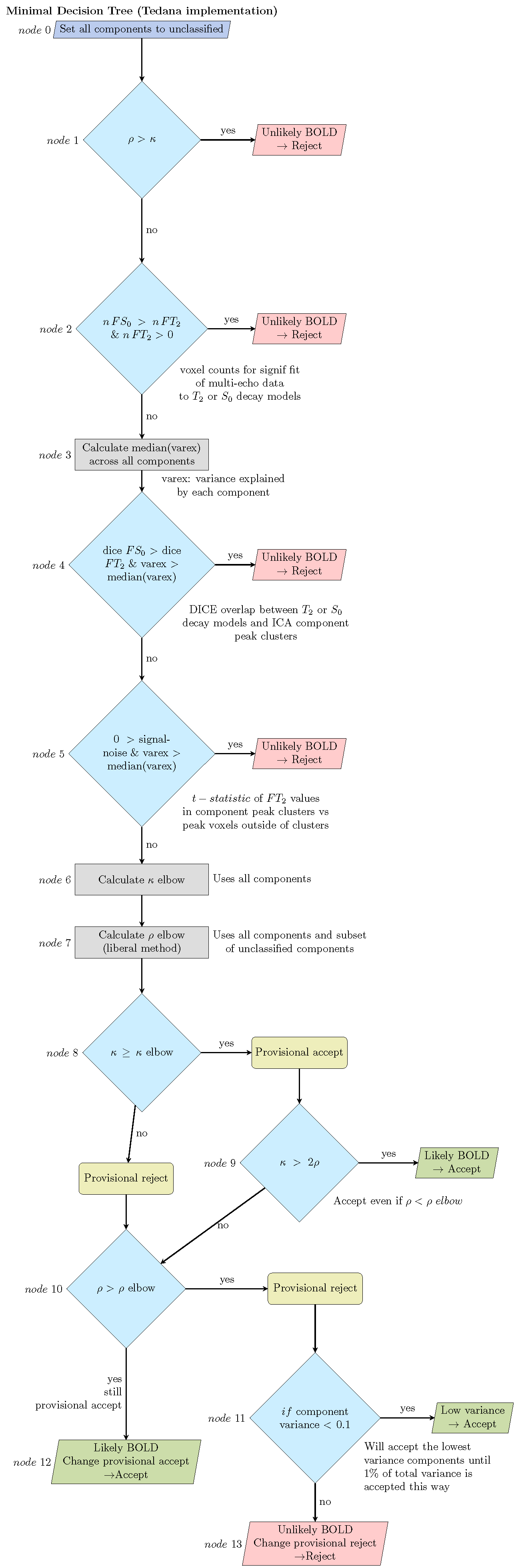
Minimal decision tree
The minimal tree starts similarly to the other trees by rejecting components
that are very unlikely to be BOLD (nodes 1-5). Then all components where
 >
>  elbow and
elbow and 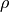 <
< 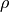 elbow
are provisional accept and otherwise are provisional reject (nodes 8 & 10).
The only expection to this is if
elbow
are provisional accept and otherwise are provisional reject (nodes 8 & 10).
The only expection to this is if  >
>  elbow and
elbow and
 > 2*
> 2* 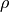 than it is provisional accept regardless of the
than it is provisional accept regardless of the
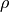 elbow under the assumption that there is enough T2* weighted signal
the component should not be rejected even if it also contains noise (node 9).
If provisional reject components have very low variance they are accepted rather
than losing degrees of freedom, but no more than 1% of the total variance can be
accepted this way (node 11). After that point, everything that is
provisional accept is accepted (node 12) and everything that is provisional reject
is rejected (node 13)
elbow under the assumption that there is enough T2* weighted signal
the component should not be rejected even if it also contains noise (node 9).
If provisional reject components have very low variance they are accepted rather
than losing degrees of freedom, but no more than 1% of the total variance can be
accepted this way (node 11). After that point, everything that is
provisional accept is accepted (node 12) and everything that is provisional reject
is rejected (node 13)